standford cs231n 2023년 버전으로 작성했습니다. 틀린 내용이 있으면 댓글로 남겨주세요~
chapter2에서는 conputer vision의 핵심분야이고, 1. The image classification task와 2. Image classification을 두 가지의 기초적인 data-driven approaches로 배우게 됩니다.
그 중 하나는 k-nearest neighbor이고 또 하나는 linear classifier을 배우게 됩니다.
Image Classification : A core task in Computer Vision

컴퓨터 비전에서 가장 중요한 것은 이미지 분류입니다.
이미지 분류(Image classification)란, 어떤 사진을 보았을 때, 그 사진들이 어떤 물체 또는 동물등인지를 분류하게 하는 것을 말합니다. 위의 사진으로 예를 든다면, 귀여운 고양이 사진을 보았을 때, 개, 고양이, 트럭, 비행기등 여러가지 선택지가 있을 때, 컴퓨터가 '이건 고양이야!'하고 말하게 만드는 것입니다. 사람들은 이런 작업들을 비교적 쉽게 수행해 냅니다.
하지만, 컴퓨터는 그러지 못합니다. 왜 그럴까요?
# Semantic Gap(의미적 차이)
semantic gap : 컴퓨터가 이미지를 볼 때 2차원이 아니라 3차원의 배열로 인식하기 때문에 생기는 문제점들이 존재합니다.

일단 컴퓨터는 우리가 사진을 보는 것처럼 사진을 보지 않습니다. 컴퓨터는 어떤 사진을 볼 때, 우리처럼 '흠, 이건 고양이 사진이군' 하며 보는 것이 아닙니다. RGB값을 나타내는 수없이 많은 숫자들의 나열로 보는 것입니다. 그렇기 때문에 컴퓨터는 이런 사진을 한눈에 알아볼 방법이 없습니다. 주변의 모든 물체가 죄다 숫자들로 보인다고 생각하면 이해가 쉬울 것 같습니다. 여러분들이 보고 있는 화면도 그냥 숫자만 있다고 생각하면, 이게 컴퓨터 화면인지 인식하기 힘들겠죠?
이미지는 정수의 텐서형태이고, 텐서라는 것은 3차원이상의 배열형태를 말하는 것입니다., 이미지의 각 픽셀은 0~255사이의 값을 가집니다. 이 값으로 색상을 표현할 수 있습니다. 고양이 그림이 컬러이기 때문에 3채널을 가지고, 흑백이라면 1채널을 가지게 됩니다. 따라서 이미지는 가로 x 세로 x RGB(색상채널)의 크기를 가지고 있습니다. 만약 가로가 400 세로가 300 컬러이미지라면, 400 x 300 x 3의 이미지 크기를 가지게 됩니다.
그 외에 다른 문제점들도 있습니다. 일단, 사진을 찍는 각도에 따라 숫자들이 죄다 바뀐다는 것입니다. 아무리 똑같은 고양이를 찍어도, 아무리 똑같은 사물을 찍어도 카메라가 살짝 오른쪽으로 간다면, 화면 자체는 비슷할 지라도 모든 숫자들 또한 살짝 오른쪽으로 가버리니 어떤 숫자들이 어떤 부분에 있다는 단순한 점만으로는 찾기는 힘듭니다.
# Challenges : Background Clutter, IIlumination, Occlusion, Deformation, Intraclass variation
딥러닝에는 Challenges들이 있습니다. 시각적인 사물(ex. 고양이)를 인식하는 이 작업은 사람이 시각적인 사물을 판단하는데에 별로 고려하지 않는데, Computer Vision알고리즘의 관점에서 바라볼 때 몇 가지 고려해볼 것들이 있습니다.
이미지 분류기는 아주 좋은 환경에서 물체를 분류할 뿐만이 아니라 다른 환경과 상황 변화에서도 변화나 오분류 없이 강인하게 물체를 분류 할수 있어야 합니다. 대표적으로 보시는 바와 같이 카메라의 시점이 변하거나, 물체의 형태나 자세, 혹은 다른 곳에 가려지거나 조명 변화 등에도 일관된 결과를 얻을수 있어야합니다.






- Viewpoint variation(시점 변화). 객체의 단일 인스턴스는 카메라와 관련하여 다양한 방식으로 방향을 지정할 수 있습니다.
- Scale variation(크기 변화). 시각적 클래스는 종종 크기가 다양합니다(이미지에서의 크기뿐 아니라 실제 세계의 크기).
- Deformation(변형). 많은 객체들은 고정된 형태가 없고, 극단적인 형태로 변형될 수 있다.
- Occlusion(가림). 객체들은 전체가 보이지 않을 수 있다. 때로는 물체의 매우 적은 부분(매우 적은 픽셀)만이 보인다.
- Illumination conditions(조명 상태). 조명의 영향으로 픽셀 값이 변형된다.
- Background clutter(배경이 복잡하다). 객체가 주변 환경에 섞여(blend) 알아보기 힘들게 된다.
- Intra-class variation(클래스 내 다양성). 분류해야할 클래스는 범위가 큰 것들이 많다. 예를 들어 의자 의 경우, 매우 다양한 형태의 의자객체가 있으며, 각각 고유한 모양들이 있습니다.
- Context(문맥 오류) 상황에 대한 정보가 없으면 데이터의 무작위 정보로 축소됩니다. 위 그림에서는 철창 그림자로인해 호랑이로 인식했지만, 실제는 개였습니다.
아무리 같은 고양이라도 조명이 다르고 숫자들은 모두 달라지고, 자세가 달라도 모두 달라지도, 어디에 숨어있으면 또 달라지고, 배경이랑 비슷하면 숫자들이 다들 비슷할 것이고 (색상값이므로), 고양이가 많으면 또 인식하기에 힘들 것입니다.
# An image classifier

그래서 이렇게 단순한 코딩으로는 이러한 문제들을 해결할 수가 없다는 것을 알게 됩니다. 가령, '1+1'을 하는 프로그램을 코딩해라!하는 것은 단순한 코딩으로 바로 답을 알 수 있겠지만, 위처럼 숫자 나열들을 주며, '자, 이제 이 숫자들이 의미하는 바가 무엇일까..? 고양이?? 개?? 한번 맟줘봐?? 같은 사이코 같은 문제는 위의 코딩처럼 단순한 코딩으로 맞출 수가 없습니다.

그래서 여러 시도들이 이루어졌습니다. 엣지 검출기로 고양이 이미지에서 엣지들을 찾고, 엣지의 코더들을 찾으면 고양이를 인식할 수 있을까요? 엣지 검출기로 추출할 수 있겠지만, 노이즈에 매우 민감하기 때문에 정확한 분류는 어려워보입니다.
# Data-Driven Approch



그래서 사람들은 'Data-Driven Approach (데이터에 기반한 접근법)'을 생각하게 됩니다. 단순히 어떤 사진을 보고 인식하는 코드를 짜는 것이 아니라, 무수히 많은 사진들과, 그 사진들이 무엇인지 알려주는 정답을 먼저 구하는 겁니다. 그 후, 머신러닝이라는 방식으로 만들어진 분류기로 사진들을 분류하면, 사진이 잘 분류되지 않을까?라는 생각입니다. 아이에게 교육하는 방식과 비슷하다고 생각하면됩니다. 우리가 아이들에게 어떻게 생긴 것들이 고양이인지 가르칠 때, 아무 고양이 사진 하나만 가지고 '이게 고양이야!'라고 하진 않습니다.
다양한 고양이 사진들을 보여주면서, '이것도 고양이, 저것도 고양이, 그리고 요것도 고양이다!'하는 방식을 통해 아이들을 가르친다면, 아이들은 훨씬 더 빠르게 어떤 것이 고양이인지 알아낼 것입니다. 바로 이런 것과 동일한 접근법이라고 생각하면 됩니다. 다시 정리해보면, Data-Driven Approach (데이터에 기반한 접근법)이란? 원하는 목표를 수행하는 확실한 알고리즘이라기 보다는 데이터에 의존하여 주어진 데이터에 따라 원하는 결과를 얻을수 있는 방향으로 조정해주는 방법입니다.
Nearest Neighbor Classifier (최근접 이웃 분류기)

그래서, 처음 생각해낸 분류법이 바로 Nearest Neighbor, 즉 '가장 가까운 이웃 찾기' 방법입니다. 말 그대로 사진들을 모두 외워서, 다른 사진을 봤을 때 지금까지 알고 있던 사진들과 비교하며, 가장 비슷하게 생긴 것을 찾아내는 겁니다. 바로, 아이들에게 '이렇게 생긴 것은 대강 고양이일 거고, 저렇게 생긴 거는 대강 배일 거야. 알겠지?? 하며 가르치는 것입니다.
# Example Dataset : CIFAR10

이렇게 가르친 때 데이터셋은 CIFAR-10이라는 데이터셋을 사용합니다. CIFAR-10 dataset는 가장 간단하면서도 유명한 이미지 분류 데이터셋 중 하나입니다. 이 데이터셋은 60,000개의 작은 이미지로 구성되어 있고, 각 이미지는 32x32픽셀크기입니다. 각 이미지는 10개의 클래스 중 하나로 라벨링되어있습니다. 예를들면, 비행기, 차, 새, 고양이등등을 나눠 놓은 데이터 뭉치입니다. 이 60,000개의 이미지 중에 50,000개는 학습 데이터셋 (training set), 10,000개는 테스트 (데이터)셋으로 분류됩니다. 위의 그림에서 각 10개의 클래스에 대해 임의로 선정한 10개의 이미지들의 예를 보여주고 있습니다.
CIFAR-10이라는 데이터 뭉치는 총 10가지 종류의 물체 혹은 동물들을 모아놓은 데이터 뭉치인데, deer, bird, plane, cat, car, airplane, automobile, dog, frog, house, ship, truck 등으로 나눠 놓은 데이터 뭉치입니다. 그리고 우리는 이 데이터 뭉치를 '컴퓨터'라는 아이에게 가져다 주어 위의 'Nearest Neighbor'라는 훈련법으로 아이에게 가르칠 겁니다. Nearest Neighbor분류기는 테스트 이미지를 통해 모든 학습 이미지와 비교를 하고 라벨 값을 예상할 것입니다. 상단 이미지의 우측과 같이 10개의 테스트 이미지에 대한 결과를 확인해보면 10개의 이미지 중 3개만이 같은 클래스로 검색된 반면, 7개의 이미지는 같은 클래스로 분류되지 않았습니다.
예를 들어, 8번째 행의 말 학습 이미지에 대한 첫번째 최근접 이웃 이미지는 붉은색의 차이입니다. 짐작컨데 이 경우는 검은색 배경의 영향이 큰 것 같습니다. 결과적으로, 이 말 이미지는 차로 잘못 분류될 것입니다.
두 개의 이미지 (이 경우에는 32 x 32 x3 크기의 두 블록)을 비교하는 정확한 방법을 아직 명시하지 않았다는 점입니다.

고양이라는 query data가 있을 때, 이 고양이라는 이미지 정보가 어떤 라벨에 적합한지 찾아내야합니다. deer, bird, plane, cat, car등 정답 라벨이 있다고 가정했을 때, 고양이(query data)는 cat(training with label)이라는 label에 제일 적합합니다. 그래서 이 둘을 비교하는 가장 간단한 방법 중 하나는 이미지를 각각 픽셀값으로 비교하고, 그 차이를 모두 더하는 것입니다.
Distance Metric
- L1 distance


그런데, 사진이 뭐가 비슷한지 어떻게 아냐고요? 바로 위의 방식으로 알 수 있습니다. 아까 전에, 컴퓨터는 사진을 볼 때, 숫자들의 나열로 본다고 이야기했었습니다. 그렇다면, 그 숫자들의 사이의 크기가 비슷하다면, 사진도 비슷하겠죠? 이런 생각을 바탕으로 사진의 숫자들을 모두 뺄 겁니다. 그리고 거기에다가 절댓값을 씌워주면? 두 숫자 사이의 거리, 즉 두 사진 사이의 다른 정도가 나옵니다. 이것은 L1 distance(L1 거리)라고 부르는데, 이 것을 사진의 모든 픽셀에 똑같이 해준 후 나온 숫자들을 모두 더해주면, 두 사진 사이의 다르 정도가 하나의 숫자로 나올 수 있습니다.
다시말해서 두개의 이미지가 주어지고, 그 것을 I1, I2 벡터로 나타냈을 때, 벡터 간의 L1 distance(L1 거리)를 계산하는 것이 한가지 방법입니다. 위의 그림은 그 과정을 시각화 한 것입니다.
다음으로는 분류기를 실제로 코드 상에서 어떻게 구현하는지 살펴보겠습니다. 첫 번째로 CIFAR-10데이터를 메모리로 불러와 4개의 배열에 저장합니다. 각각은 학습(training) 데이터와 그 라벨, 테스트 데이터와 그 라벨입니다. 아래 코드에 Xtr(크기 50,000 x 32 x 32 x 3)은 training set의 모든 이미지를 저장하고, 1차원 배열인 Ytr(길이 50,000)은 트레이닝 데이터의 라벨 (0부터 9까지)를 저장합니다.
Xtr, Ytr, Xte, Yte = load_CIFAR10('data/cifar10/') # 제공되는 함수
# 모든 이미지가 1차원 배열로 저장된다.
Xtr_rows = Xtr.reshape(Xtr.shape[0], 32 * 32 * 3) # Xtr_rows는 50000 x 3072 크기의 배열.
Xte_rows = Xte.reshape(Xte.shape[0], 32 * 32 * 3) # Xte_rows는 10000 x 3072 크기의 배열.
이제 모든 이미지를 배열의 각 행들로 얻었습니다. 아래에는 분류기를 어떻게 학습시키고 평가하는지에 대한 코드입니다.
nn = NearestNeighbor() # Nearest Neighbor 분류기 클래스 생성
nn.train(Xtr_rows, Ytr) # 학습 이미지/라벨을 활용하여 분류기 학습
Yte_predict = nn.predict(Xte_rows) # 테스트 이미지들에 대해 라벨 예측
# 그리고 분류 성능을 프린트한다
# 정확도는 이미지가 올바르게 예측된 비율로 계산된다 (라벨이 같을 비율)
print 'accuracy: %f' % ( np.mean(Yte_predict == Yte) )
일반적으로 평가 기준으로서 accuracy(정확도) 를 사용합니다. 정확도는 예측값이 실제와 얼마나 일치하는지 그 비율을 측정합니다. 앞으로 만들어볼 모든 분류기는 공통적인 API를 갖게 될 것입니다.: 데이터(X)와 데이터가 실제로 속하는 라벨(y)을 입력으로 받는 train(X,y) 형태의 함수가 있다는 점입니다. 내부적으로, 이 함수는 라벨들을 활용하여 어떤 모델을 만들어야 하고, 그 값들이 데이터로부터 어떻게 예측될 수 있는지를 알아야 합니다. 그 이후에는 새로운 데이터로 부터 라벨을 예측하는 predict(X) 형태의 함수가 있습니다. 물론, 아직까지는 실제 분류기 자체가 빠져있다. 다음은 앞의 형식을 만족하는 L1 거리를 이용한 간단한 최근접 이웃 분류기의 구현입니다.
# Implementation of a simple nearest neighbor classifier using L1 distance
import numpy as np
class NearestNeighbor(object):
def __init__(self):
pass
def train(self, X, y):
""" X is N x D where each row is an example. Y is 1-dimension of size N """
# nearest neighbor 분류기는 단순히 모든 학습 데이터를 기억해둔다.
self.Xtr = X
self.ytr = y
def predict(self, X):
""" X is N x D where each row is an example we wish to predict label for """
num_test = X.shape[0]
# 출력 type과 입력 type이 갖게 되도록 확인해준다.
Ypred = np.zeros(num_test, dtype = self.ytr.dtype)
# loop over all test rows
for i in xrange(num_test):
# i번째 테스트 이미지와 가장 가까운 학습 이미지를
# L1 거리(절대값 차의 총합)를 이용하여 찾는다.
distances = np.sum(np.abs(self.Xtr - X[i,:]), axis = 1)
min_index = np.argmin(distances) # 가장 작은 distance를 갖는 인덱스를 찾는다.
Ypred[i] = self.ytr[min_index] # 가장 가까운 이웃의 라벨로 예측
return Ypred
이 코드를 실행해보면 이 분류기는 CIFAR-10에 대해 정확도가 38.6% 밖에 되지 않는다는 것을 확인할 수 있습니다. 임의로 답을 결정하는 것(10개의 클래스가 있으므로 10%의 정확도)보다는 낫지만, 사람의 정확도(약 94%)나 최신 컨볼루션 신경망의 성능(약 95%)에는 훨씬 미치지 못합니다. (CIFAR-10에 대한 최근 Kaggle 대회 순위표 참고).
거리(distance) 선택 벡터간의 거리를 계산하는 방법은 L1 거리 외에도 매우 많습니다. 또 다른 일반적인 선택으로, 기하학적으로 두 벡터간의 유클리디안 거리를 계산하는 것으로 해석할 수 있는 L2 distance(L2 거리) 의 사용을 고려해볼 수 있다. 이 거리의 계산 방식은 다음과 같습니다.:
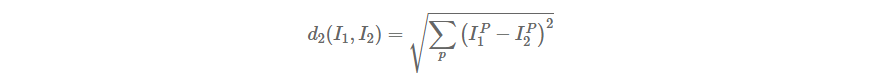
즉, 이전처럼 각 픽셀간의 차를 구하지만 각각에 제곱을 취하고, 전부 더한 다음에 최종적으로 제곱근을 취한다. NumPy를 사용한다면 위 코드를 사용하여 거리를 계산하는 아래의 코드 부분 딱 한 줄만 바꾸면 됩니다!
distances = np.sqrt(np.sum(np.square(self.Xtr - X[i,:]), axis = 1))
위 코드에서는 np.sqrt 함수를 호출하는 것을 그대로 남겨두었지만, 제곱근 함수는 monotonic function이기 때문에 실제 nearest neighbor 응용에서 제곱근은 빼도 결과에 상관이 없습니다. 즉, 계산되는 거리들의 크기에는 차이가 생기겠지만 그 순서는 동일하기 때문에, 제곱근 함수를 포함할 때와 포함하지 않을 때의 nearest neighbor(최근접 이웃)는 동일합니다. 이 거리 함수를 사용하여 Nearest Neighbor 분류기를 CIFAR-10 데이터셋에 돌린다면, 35.4% 정확도를 얻을 수 있었습니다. (L1 거리를 사용한 결과보다 조금 낮아졌다).
L1 vs. L2. 두 거리 함수의 특징을 비교하는 것은 매우 흥미로운 주제입니다. 일반적으로, L2 거리는 L1 거리에 비해 두 벡터간의 차가 커지는 것에 대해 훨씬 더 크게 반응합니다. 즉, L2 거리는 하나의 큰 차이가 있는 것보다 여러 개의 적당한 차이가 생기는 것을 선호합니다. L1/L2 거리(또는 두 이미지의 차에 대한 L1/L2 norm)는 일반적인 p-norm의 형태 중 가장 많이 사용되는 두 가지입니다.
그러면, 이제 한번 아이에게 분류하는 법을 가르쳐 볼까요? 일반적으로, 아이를 가르칠 때에는 두 가지 방법으로 나누어 줍니다. training(훈련)부분과 predict(예측)부분입니다.
이제 부분별로 살펴 봅시다!!
def train(self, X, y):
""" X is N x D where each row is an example. Y is 1-dimension of size N """
# the nearest neighbor classifier simply remembers all the training data
self.Xtr = X
self.ytr = y
첫 번째는, training(훈련) 부분입니다. 그리고 아까도 말했듯이, Nearest Neighbor에게 train은 그저 사진들을 외우는 것일 뿐입니다.
def predict(self, X):
""" X is N x D where each row is an example we wish to predict label for """
num_test = X.shape[0]
# lets make sure that the output type matches the input type
Ypred = np.zeros(num_test, dtype = self.ytr.dtype)
# loop over all test rows
for i in range(num_test):
# find the nearest training image to the i'th test image
# using the L1 distance (sum of absolute value differences)
distances = np.sum(np.abs(self.Xtr - X[i,:]), axis = 1)
min_index = np.argmin(distances) # get the index with smallest distance
Ypred[i] = self.ytr[min_index] # predict the label of the nearest example
그리고, predict(예측) 부분입니다. 아이에게 지금까지 봤던 사진이 아닌 다른 사진을 주면서, '이게 뭘까~?' 하는 것이죠. Nearest Neighbor는 predict작업은 사진을 보고, 지금까지 외웠던 사진들의 숫자들로 빼 주는 것입니다.
'개 사진들이랑 뺐을 때는.. 평균 100만큼 차이나고, 고양이 사진들이랑 뺐을 때는, 평균 200만큼 차이가 나네! 그러면 아마 이 사진은 고양이보다는 개에 더 가까울 거야!' 라고 생각하는 과정이, 바로 Nearest Neighbor의 predict 과정입니다.
그런데 문제가 있습니다. 이것을 외우는 데는 시간이 엄청나게 빨리 걸립니다. 아, 사람이 외울 때는 당연히 오래 걸리겠지만, 우리의 아이는 엄청난 기억력을 가진 컴퓨터라는 아이니깐, 순식간에 외울 수 있습니다.
하지만, 이것을 예측하는 것은 꽤나 오랜 시간이 걸립니다. 아이가 지금까지 50000개의 사진을 외웠다면, 그 모든 사진들을 죄다 빼주면서 계산을 해야 하니까요. 단순히 연산이 50000번인 것도 아니고, 50000개의 사진의 모든 숫자들을 다 빼서 더하고, 평균을 내고... 을 해야 하니까요.
근데 이게 왜 문제냐고요? 만약 우리가 개나 고양이 사진을 찍어서, 이게 개인지 고양이인지 구분하는 프로그램을 만들었는데, 사진 하나 찍고 이게 개인지 고양이인지 구분하려고 보니깐 1시간이 걸린다고 하네요! 그러면, 여러분들이라면 과연 이 프로그램을 사용할까요? 그렇지 않겠죠..?
그렇기 때문에, 훈련에 걸리는 시간은 오래 걸려도 별로 상관이 없습니다. 이 훈련은 한 번만 하면 다음부터 사용할 때에는 그 정도의 시간은 걸리지 않으니까요. 하지만, 예측 단계에서 이렇게 느리면.. 그것은 문제가 생긴다는 것입니다.
Q. N개의 examples를 들면, 얼마나 빨리 훈련하고 예측을할까요?
A. Train O(1), Predict O(N)
하지만 이것은 좋지 못합니다. 우리가 원하는 분류기는 예측을 빨리하고, 훈련을 느리게 하는 분류기입니다.
빠르고, 대략적으로 근사하게 nearest neighbor에 대한 많은 방법이 존재합니다. (cs231n을 넘어서)
(참고 : https://github.com/facebookresearch/faiss)

색깔은 개나 고양이 같은 사진의 종류를 말하고, 점들은 사진을 말합니다. 즉, '형아, 저기 점 주변에 찍히는 다른 점들은 내가 배경으로 색칠해놓은 색의 사진일 거야. 그렇지?'라고 말하는 것이죠. 근데, 과연 그럴까요?
가운데 노란색 부분을 봅시다. 직관적으로 봤을 때, 뭔가 저 노란색 주변에 있는 점들은 초록색이어야 할 것 같은 느낌, 안 드시나요? 아무래도 초록색으로 둘러싸여 있는데, 저 점 하나 때문에 그 부분만 노란색 부분이 된다는 것은, 약간 무리가 있어 보입니다.
여태까지 예측을 할 때 가장 가까운 이미지의 라벨만을 사용하는 것을 이상하다고 생각할 수도 있을 것입니다. 확실히, k-Nearest Neighbor Classifier (kNN 분류기) 라는 것을 사용한다면 거의 무조건 더 분류를 잘 할 수 있습니다. 아이디어는 매우 간단합니다: 학습 데이터셋에서 가장 가까운 하나의 이미지만을 찾는 것이 아니라, 가장 가까운 k 개의 이미지를 찾아서 테스트 이미지의 라벨에 대해 투표하도록 하는 것입니다. 여기서 k = 1 인 경우, 원래의 Nearest Neighbor 분류기가 된다. 직관적으로 k 값이 커질수록 분류기는 이상점(outlier)에 더 강인하고, 분류 경계가 부드러워지는 효과가 있습니다.
# K-Nearest Neighbors

그래서 고안된 방법이 K-Nearest Neighbor 방법입니다. 가장 가까운 사진을 찾는 건 그대로이지만, 주변 K개를 봤을 때 가장 비슷한 것이 바로 정답일 거라는 생각인 것이죠.
위의 사진에서 그것이 가장 잘 보입니다. K=1이었을 때는, Nearest Neighbor와 정말히 똑같은 그림이 그려집니다. 하지만, K=3, K=5 일때는 초록색 부분의 가운데 배경 색이 초록색으로 바뀌었고, 위에 삐죽 튀어나왔던 부분도 파란색과 보라색으로 바뀐 것을 볼 수 있습니다. 직관적으로 k 값이 커질수록 분류기는 이상점(outlier)에 더 강인하고, 분류 경계가 부드러워지는 효과가 있습니다.
# K-Nearest Neighbors: Distance Metric

아까 전에 L1 distance라고 이야기했던 것 기억나시나요? 그것 대신, L2 distance라는 친구를 사용해서 두 사진 사이의 차이를 알아내 볼 겁니다. 정확한 수식은 잘 모르셔도 됩니다. 그저, 거리를 재는 다른 방법이라는 생각과, 대충 거리를 그림으로 나타내면 위처럼 L1은 다이아몬드, L2는 원 형태가 나온다는 정도만 아시면 될 것 같습니다. 위에 그림에서 k=1일 때, L1 또는 L2를 사용해서 훈련했을 때 컴퓨터가 그려낸 사진입니다.
http://vision.stanford.edu/teaching/cs231n-demos/knn/
http://vision.stanford.edu/teaching/cs231n-demos/knn/
vision.stanford.edu
위의 링크에 들어가시면, 직접 k값과 거리(L1, L2)를 바꾸면서 종류 갯수도 바꾸면서 어떤 그림이 그려지는지 확인해보시면 이해가 되실 것 같습니다.
실제 문제를 적용할 경우, 대부분은 NN분류기보다 k-nearest Neighbor(kNN)분류기를 사용하고 싶어할 것입니다. 그러나 어떤 k값을 골랴야할까요? 이 문제에 대해 지금부터 다루겠습니다.
# Hyperparameter 튜닝을 위한 검증 셋 (Validation set)
위에서 잠깐 해보았으면, '그럼, K랑 distance는 어떤 게 가장 좋은 거야??'라는 생각이 드셨을지 모르겠습니다. K와 distance는 우리가 직접 정해야 하는 값, 즉 Hyperparameter(하이퍼파라미터) 입니다. 이에 대한 정답은 간단합니다.
상황마다 다릅니다! 그리고, 직접 하나하나 넣어 보면서, 어떤 것이 가장 정답률이 높은 지를 알아내는 것이 중요하죠.
hyperparameter이라는 말은 앞으로도 굉장히 자주 나올 말이니까, 숙지해 두는 것이 좋을 것 같습니다.

그렇다면, 이 hyperparameter들을 제대로 맞추는 방법을 알아봅시다. 가장 먼저 드는 생각은, '아니, 그냥 내 데이터셋에다가 집어넣어서, 제일 잘 작동되는 거 고르면 되는거 아니야??' 일 것 같습니다.
하지만, 이렇게 해버리면 문제가 생겨버립니다. 아까 위의 사진을 다시 생각해 봅시다. 다른 사진이 들어오지 않을 때에, K=1이 가장 우리의 데이터셋에서 좋은 효과를 내고 있다고 볼 수 있었을 것입니다. 하지만, 다른 사진이 들어갈 때에는, 약간 문제가 생겼죠? 즉, 우리가 진정으로 원하는 것은, 우리가 가지고 있는 데이터셋에서 작동이 잘 되는 것이 아니라, 그냥 진짜로 찍은 사진에 작동이 잘 되는 것을 찾고 싶은 것이죠.
그러면, 다음 생각은 '아니.. 그럼 train과 test로 나눈 후에, test에 잘 되는 놈으로 하지!' 일 것입니다. 하지만, 그것마저도 별로 좋은 선택은 아닙니다. train에서 훈련된 것을 test에서 확인을 한 후에, test값에 적절한 k 또는 distance 값을 바꾸어 주더라도, 결국엔 test 셋에서만 잘 되는 것일 수도 있고, 아예 새로운 데이터가 들어왔을 때는 또 어떻게 반응할지 모르기 때문이죠.
그럼, 다른 좋은 생각 없을까요? 한번, 데이터셋을 세 부분으로 나누어 봅시다. train, validation, test로 말이죠.
train 데이터셋에서 열심히 훈련된 값을, validation 데이터셋으로 확인하며 hyperparameter를 바꾸어 주고, test는 마지막 딱 한 번만 만져 보는 것이죠. 이렇게 되면, test 셋은 마치 우리의 데이터셋 안에 없는, 세상에서 아예 새로운 데이터가 되는 셈이고, 그렇다면 우리가 원하던 '진짜 새로운 데이터에서의 테스트'를 해 볼 수 있게 되는 것이죠.

그리고, Cross-Validation이라는 방식도 존재합니다. 일단 큰 거 하나와, 작은 거 하나 총 두개로 먼저 나눕니다. 그 후, 작은 거는 test 셋으로 설정하고, 큰 거 하나를 놓고 다시 여러 개로 나누어서, 첫 번째 부분만 val로 놓고, 나머지를 train으로 놓은 뒤에 hyperparameter를 설정하고, 다시 두 번째 부분만 val로 놓고, 나머지를 모두 train으로 놓은 뒤에 hyperparameter를 설정하고..
이런 방식으로 해서, 그 결과의 평균값으로 hyperparameter를 설정하는 것입니다. 혹시 validation을 나눈 것이 이상하게 나누어져 제대로 되지 않을 수도 있으니, 이런 식으로 hyperparameter를 정해 보는 것이죠. 이렇게 한다면, 더욱더 확실하게 hyperparameter의 값을 구할 수 있을 것입니다.
하지만, 딥러닝에서 자주 사용되는 기술은 아닙니다. 이후에 나올 training 들은, 연산을 굉장히 많이 해야 하므로, 저렇게 하나하나 다 해보는 데에는 너무 오래 걸리고, 힘이 들기 때문이죠.
# Setting Hyperparameters

그렇다면, 이런 식으로 설정된 hyperparameter들을 한번 비교해 봅시다. 그래프의 가로축은 k의 값이고, 세로축은 test에서의 정확도 값입니다. 그래프를 보시면 아시겠지만, k가 대충 7 정도일 때 가장 높은 정확도를 보이는 것을 확인할 수 있습니다. 즉, k를 7 정도로 사용하는 것이 가장 효율적일 것이라는 거죠.
주의하셔야 할 점은, 이렇게 나온 hyperparameter들은 문제 및 데이터셋마다 모두 다르다는 것입니다. 같은 방식으로 훈련을 하더라도, '이 사진을 보고 개인지 고양이인지 구별하시오'라는 문제에 최적화된 hyperparameter의 값과 '이 사진을 보고 웃는 얼굴인지 우는 얼굴인지 구별하시오'라는 문제에 최적화된 hyperparameter의 값이 다르다는 것이죠. 즉, 이러한 과정은 모든 데이터셋과 문제들마다 한 번씩 거쳐가며 설정하는 것이 좋다는 것입니다.

CIFAR-10을 K-Nearest Neighbor로 훈련시킨 결과입니다. 왼쪽은 정답 종류를 의미하는 사진, 오른쪽은 훈련된 컴퓨터가 고른 예측입니다. 멀리서 보면 꽤나 잘 맞춘 것으로 볼 수도 있습니다. 실제로 사진이 다 비슷하게 생겼기 때문이죠. 특히, 개구리 (위에서 4번째) 사진들은 죄다 배경의 흰색 계열로써, 사진 전체적으로 굉장히 비슷하죠. 하지만, 그것만 비슷할 뿐, 자세히 보면 완전 틀린 답들을 골라내고 있습니다. 사진이 비슷하긴 하지만, 그렇다고 그것이 정답이라는 보장은 없으니깐 말이죠.

하지만, 지금까지 열심히 공부했던, Nearest Neighbor이라는 방식은 절대로 사용되지 않습니다.
우선, 초반에도 언급한 predict 과정이 굉장히 오래 걸린다는 것과, 사진 사이의 distance는 사실 그렇게 의미 있는 값이 아니라는 것 때문이죠.
예를 들어, 위의 Boxed, Shifted, Tinted 사진은 왼쪽의 원본 사진과 같은 L2값을 가지고 있다고 합니다. 즉, 이것으로 학습을 한다면 얼굴에 박스가 쳐져있던, 색이 바래졌든 간에 같은 사진으로 생각해 버린다는 것이죠.
또한, 저---위에 Lecture 2 - 30에서 보았을 때에도 잠깐 언급했지만, 사진이 비슷하게 생겼다고 해서 비슷한 물체인 것은 아닙니다. 갈색 조명으로 갈색 느낌을 준 축구공과, 갈색 농구공은 비슷하게 생겼지만 다른 공인 것처럼 말이죠.
# Curse of dimensionality

더 큰 문제로는, 차원이 넓어질수록 필요한 데이터의 개수가 기하급수적으로 많아집니다. 1차원일 때에는 4개만 필요하면 데이터의 개수가, 2차원이 되면 4*4=16개가 필요해지고, 3차원이 되면 4*4*4=64개가 필요해지니까요.
'오잉? 생각보다 적네?'라고 생각하실지 모르겠지만, 실제로는 이것보다 훨씬 큰, 100000 같은 수가 1차원에 필요하다 하면, 2차원은 10000*10000,, 3차원은 10000*10000*10000개가 필요하니... 정말 정말 많아지는 것을 볼 수 있습니다.
# Summary
그럼.. 우리 지금까지 허튼짓 한 거냐고요?? 어차피 안 쓸 거 왜 알려줬냐고요?
그 질문을 하기 전에, 일단 이것을 배우는 과정을 통해 배운 것들을 확인해봅시다. 우선, 이미지 분류에는 트레이닝 이미지와 그에 맞는 카테고리들이 필요하고, test 셋에서 그것을 predict 해야 한다는 것을 알았습니다.
K-nearest는 그 카테고리, 라벨들을 가장 가까운, 유사한 training 셋의 사진으로 맞춘다는 것도 알았고, distance(L1, L2)와 K값은 hyperparameter(하이퍼파라미터)라는 것이라는 것도 알았고, hyperparameter를 고를 때에는 validation 셋에서 골라야 하고, test 셋에서 맨 마지막 딱 한번 돌려봐야 한다는 것도 알았습니다!
nearest neighbor라는 가장 단순한 알고리즘으로, 우리는 앞으로 배워나갈 인공지능에 대한 기본적인 지식들을 깨달을 수 있었습니다. 그럼 다음으로 넘어가서, 지금 배운 것을 써먹어봅시다!
'Deep Learning > cs231n' 카테고리의 다른 글
| 쉽게 풀어쓴 cs231n 2강 svm, softmax loss function(3) (1) | 2023.11.24 |
|---|---|
| 쉽게 풀어쓴 cs231n 2강 Linear Classifier(2) (1) | 2023.11.23 |
