이번 포스팅에서는 이전 장에 이어 stanford univ. cs231n 2강의 뒷 부분에 대해 포스팅해보려고 합니다. 뒷부분의 내용은 linear classifier, softmax, svm에 대한 내용들로 이루어져 있습니다~ 제가 이 내용들을 최대한 쉽게 풀어서 설명해보겠습니다.
# Linear Classifier
2강 (1)번포스팅에서는 knn으로 이미지 분류방법을 소개했는데, 이번에는 knn이 아닌 다른 이미지 분류 기법으로 선형 분류기와 신경망 모델에 대해 살펴보겠습니다. 신경망(Neural Network) 모델은 선형 분류기들을 층(Layer)으로 연결한 것이라고 할 수 있습니다.

선형 분류기(Linear Classifier)는 주어진 데이터를 가장 잘 분류하는 선형 함수를 구하여, 새로운 입력 데이터가 어디에 속하는지 판별할 수 있는 모델입니다. 그렇다면 왜 선형이라고 부를까요? 선형 시스템의 성질(중첩의 원리)를 따르며, 다차원 공간상에서 직선의 형태를 띄기 때문입니다.
선형 시스템의 성질(중첩의 원리)에 대해 잘 모르시는 분들을 위해 설명드리면, 중첩의 원리는 어떠한 시스템에서 두 개의 서로 다른 입력을 동시에 가했을 때 얻어지는 출력은, 두 개의 입력을 각각 따로 가했을 때 얻어지는 출력들의 합과 같다는 것입니다. 좀 더 자세한 내용은 선형이 뭐고? 비선형이 뭘까? 이 포스팅을 참고해주세요.
이미지를 분류하기 위해 데이터셋이 필요합니다. 그래서 예제 데이터셋으로 CIFAR-10을 사용하겠습니다. CIFAR-10은 10개의 라벨(클래스)로 이루어져있기 때문에 10이라는 숫자가 붙여졌습니다. 50,000개 훈련 이미지들의 각각 이미지는 32 x 32 x 3의 크기를 같습니다. 32 x 32 x 3는 각각 [가로크기 x 세로크기 x 색상채널의 수]로 의미합니다. 그리고 10,000장의 테스트 이미지가 들어가 있고 총 60,000장으로 이루어진 데이터 셋입니다.

# Parametric Approach: Linear Classifier
우리가 앞에서 살펴본 Nearest Neighbor는 파라미터가 들어가지 않습니다. 다시 말해 non-parametric Approach입니다. 한국어로 비모수적 방법이라고 합니다. 하지만 앞으로 배울 모델들은 Parametric approach입니다. 모델 설명이전에 Parametric Approch와 Non-parametric Approach에 대해 비교하고 넘어가겠습니다.
Parametric approach와 Non-parametric Approach 두 접근 방식 모두 알려지지 않은 함수 f를 추정해야합니다. 다시말하면, 우리는 독립변수 X(즉, 입력집합)과 종속 변수 Y(즉, 목표 변수)사이의 매핑 함수를 아래와 같이 학습해야 합니다.

알려지지 않은 함수를 추정하기 위해, 데이터(더 정확히는 훈련 데이터)에 모델을 맞추어야 합니다. 추정하려는 함수 형태는 일반적으로 알려지지 않으므로, 목표 함수 f의 형태에 대한 가정을 하거나 다양한 모델을 적용해야할 수 있습니다. 일반적으로 이 과정은 모수적(parametric) 또는 비모수적(non-parametric)일 수 있습니다.
parametric방법에서 일반적으로 함수 f의 형식에 관해 가정합니다. 예를 들어, 미지의 함수 f가 선형이라고 가정할 수 있습니다. 즉, 함수는 아래와 같은 형식이라고 가정합니다.

여기서 f(x)는 추정할 미지의 함수, w는 학습할 계수, p는 독립변수의 수, x는 해당 입력입니다. 이제 추정할 함수의 형태에 대해 가정하고 이 가정에 맞는 모델을 선택했으므로 결국 모델을 학습하고 계수를 추정하는데 도움이 되는 학습과정이 필요하게 됩니다. 요약하자면, 머신러닝의 parametric 방법은 일반적으로 추정할 함수의 형태에 대한 가정을 하고, 이 가정을 기반으로 적절한 모델을 선택하여 모델 parametric들을 추정하는 모델 접근 방식을 취합니다.

함수 f(x, W)에서 x는 주어진 이미지이고, 우리가 컨트롤을 전혀 할 수 없는 부분이고, 우리가 컨트롤을 해야하는 부분은 W(weight) 파라미터입니다. 그래서 3072개의 숫자로 구성된 하나의 이미지가 입력되었을 때, 그 출력 값으로 어떤 클래스에 속하는지 열 개의 숫자를 반환해주는 방식을 취하고 있습니다. 그 이유는 우리가 사용하는 데이터셋이 cifar-10이고 이 데이터셋은 10클래스로 구성되어있기 때문입니다.

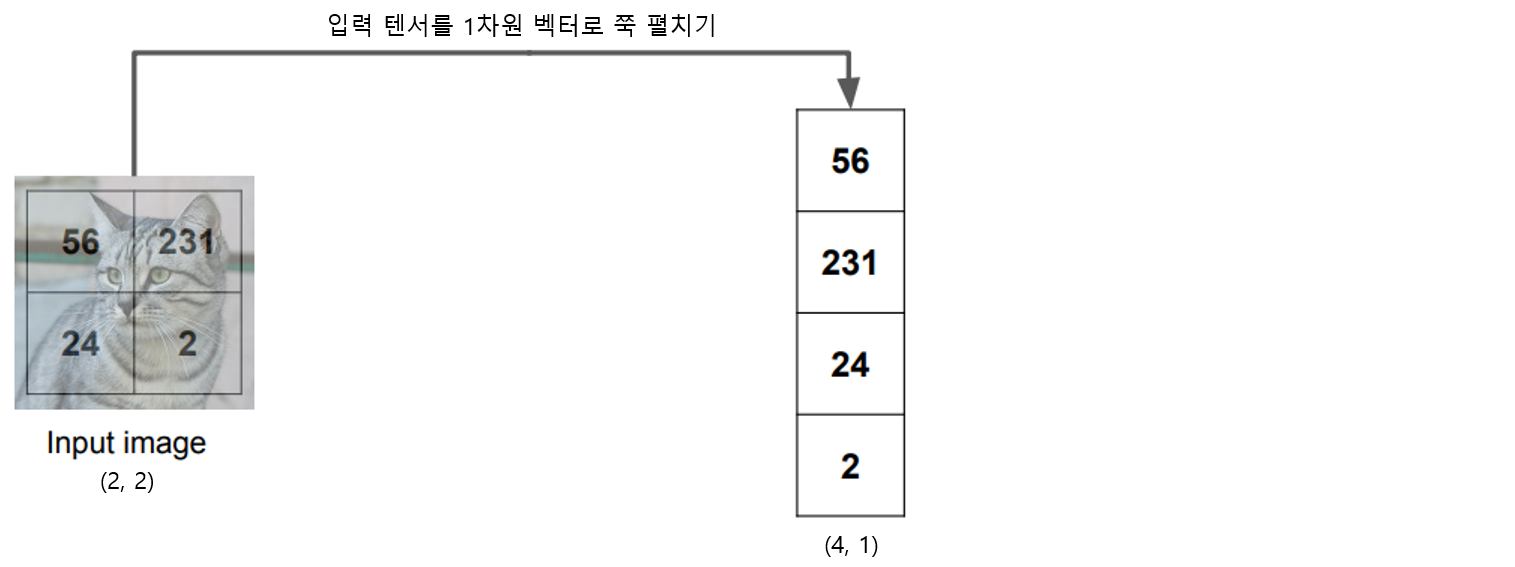
그래서 우리가 추정할 함수 f(x,W)을 WX 선형모델이라 가정하면, x는 고양이 이미지가 들어가고, 출력은 10클래스의 각 점수가 출력되야합니다. 그러면 [32 x 32 x 3]크기의 고양이 이미지를 입력(x)에 넣기 위해 1차원 벡터로 쭉 펼쳐서 [3072 x 1]로 형태를 변형해주고, 출력f(x,W)은 클래스의 크기로 맞춰줍니다. 10개의 클래스를 분류하는 문제이기 때문에 f(x,W)의 크기는 [10x1]입니다.



입력과 출력이 주어진 상태에서, 어떤 W를 곱해야 출력 [10x1]크기가 되는지 그에 맞는 W크기를 찾아야합니다. 선형대수를 공부하셨더라면, W는 [10 x 3072]크기가 되어야지만, 입력 [3072 x 1]을 곱해서 출력 [10 x 1]크기로 반환되는 것을 알 수 있습니다.

즉 W차원은 우리가 맞춰줘야합니다. 결과적으로 우리가 컨트롤 해야할 대상은 총 3만 7120개의 weight이 됩니다. 그러니까 우리들은 이 W, 즉 weight = parameter들을 컨트롤 해야하기 때문에 이러한 접근 방법을 parametric approach다라고 말합니다.

여기서 생략한 것이 있는데 그것은 b(bias)입니다. bias 또한 파라미터입니다. 그러기 때문에 최적의 값을 찾아내야합니다. 그래서 모델에서 파라미터라 함은 W와 b를 부르는 것이고, 이들은 학습을 통해 최적의 값을 찾아내야합니다.
# 모델에서의 Linear classifier역할
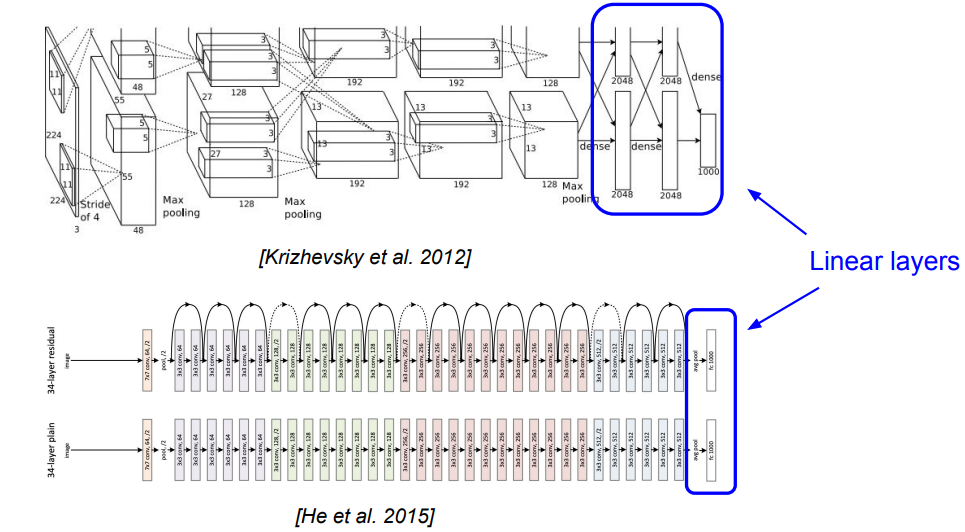
이런 Linear layer들은 모델의 맨 끝단에 위치하며, 이전 layer에서 얻었던 feature들을 바탕으로 클래스를 분류하기 위한 학습을 수행합니다. 1000개의 클래스를 분류해야한다면, [1000 x 1]의 크기로 선형변환을 수행하여 각 클래스의 점수를 학습합니다.
# Algebraic Viewpoint (대수학 관점)
선형분류기를 직관적으로 이해하기 위해 대표적인 관점으로 대수적 관점이 있습니다. 예를들어 이미지 4픽셀을 가지고, 3개의 클래스(고양이/개/배)를 가지는 예제에 대해서 생각해봅시다.

대수적 관점에서의 선형 분류기는 행렬 곱과 오프 셋의 합으로 이루어집니다.
# 선형분류기의 예측이 선형적인 이유?
선형분류기의 예측이 선형적인 이유에 대해 살펴보겠습니다. 편향 b를 무시하고, 선형 분류기 f(x,W)를 입력이미지 x에 스케일링 계수 c를 곱하여 입력으로 사용합니다. 출력 결과 또한 기존의 출력에 c가 곱해진 결과가 나옵니다. 입력을 c배 했을 때, 출력이 기존 출력의 c배 한 것과 동일 한 것이 선형 시스템의 조건으로 중첩의 원리라고 부릅니다.


# Visual Viewpoint
지금까지 선형분류기를 대수적 관점에서 보았으나, 다른 관점에서 살펴봅시다. 대수적 관점에서는 이미지를 직렬화, 쭉 펼친 벡터, 일렬로 나열해서 가중치 행렬과 곱을 수행하였습니다. 행렬을 입력 이미지와 동일한 형태로 다뤄볼 수 있습니다. 그렇게 되면, 가중치와 편향이 클래스별로 분할됩니다.

선형 분류기의 가중치 행렬을 시각화 시키면 대수적으로 풀었을 때보다 직관적으로 이해할 수 있습니다. 선형분류기가 카테고리당 하나의 탬플릿(가중치 행렬)을 가지므로 탬플릿 매칭이라 할 수 있습니다. 학습된 템플릿은 해당 카테고리와 유사하게 보입니다.

하나의 탬플릿만으로 데이터의 여러가지 경우를 다룰 수 없습니다. 예시로 말 템플릿이 한 개만으로 부족할 때 어떻게 해야할까요? 어떤 경우는 왼쪽에 서있거나, 오른쪽에 서있는 경우, 혹은 정면을 보는 경우 다른 방향을 보는 경우등등 있을 것 같습니다.

# Geometric Viewpoint
시각적 관점 다음으로 이미지의 기하학적 구조를 살펴볼 수 있습니다. 아래의 그래프는 x 축에 특정 픽셀 값, y에는 픽셀 값 변화에 따른 분류기의 점수 변화입니다. 선형 분류기를 사용하므로, 분류기 점수는 선형적으로 변화하게 됩니다.

여러 픽셀을 동시에 살펴보기위해, x 축에 한 픽셀의 값, y 축에는 다른 픽셀 값을 놓습니다. x 픽셀의 값이 변함에 따라, y 픽셀의 값도 동시에 변화합니다. 그 이유는 선형 시스템이므로 차량 점수는 픽셀들의 값이 증가 시 아래의 직선과 직교하는 방향으로 선형적으로 증가합니다.

차량 템플릿 뿐만이 아니라 다른 템플릿들도 픽셀 값의 변화에 따라 선형적으로 증감하게 됩니다. 아래와 같이 이미지의 두 픽셀만 가지고 보는건 직관적이지는 않지만, 이 개념을 고차원으로 확장하면 선형 분류기는 유클리디안 공간상에서의 초평면으로서 카테고리를 분류하는데 사용될 수 있습니다. 기하학적 관점이 선형 분류기를 이해하는데 유용하지만, 3차원 공간에서 살고있는 우리는 고차원을 이해하기는 어려울 수 있습니다.

# 선형 분류기로 분류하기 힘든 경우
아래의 3가지의 경우 선형 분류기로 올바르게 분류할 방법이 존재하지 않습니다.

1) parity problem(반전성 문제) - 홀, 짝수를 분류할 때, 0보다 큰 픽셀의 수가 홀수, 짝수 일 때 분별하는 것입니다. 예를 들면 (1,1) -2 / (1, 0) -1/ (-1,-1) -0 이다. 단순히 선 하나로 분류 할 수 없습니다.
2) Multimodal problem - 한 클래스가 다양한 공간에 분포하는 경우, 클래스가 다양한 공간에 분포하는 경우, Linear classifier로 해결하기 어렵습니다. 파란색의 섬들이 분포하고 그 의외의 구간은 모두 빨간색입니다.
여기까지 llinear classifier에 대한 포스팅을 마무리하겠습니다~ 다음 포스팅에서는 2023년버전 chap2슬라이드의 대망의 마지막 부분인 svm와 softmax에 대해 살펴보겠습니다. 포스팅 읽고 이해가 안가는 내용이나 틀린내용은 과감하게 댓글로 써서 소통하면 좋겠습니다. 고생하셨습니다 :)
# reference
https://towardsdatascience.com/parametric-vs-non-parametric-methods-2cea475da1a
'Deep Learning > cs231n' 카테고리의 다른 글
| 쉽게 풀어쓴 cs231n 2강 svm, softmax loss function(3) (1) | 2023.11.24 |
|---|---|
| 쉽게 풀어쓴 cs231n 2강 Image Classification과 KNN(1) (3) | 2023.11.20 |
